ここ数年担当している学生実習の中で、研究に携わったことがなくExcelもほとんど触ったことのない学生が、グラフを作ったり統計学的な検定をしたりする作業を指導する機会があります。
Excelでグラフを作成して、統計学的な検定を行いたいけど、どこから手をつければいいかわからない…
そんな学生に向けて、この記事では研究や実験で集めたデータを使ってExcelで可視化し、統計学的に分析する方法を図を交えてわかりやすく解説します。
この記事で学べること:
- Excelの基本操作
- 棒グラフ・エラーバーの作成方法
- 3群比較に必要な統計学的な検定(F検定、t検定など)の方法
- 多群比較(3群以上)に必要な統計学的な検定(Tukey の方法、Dunnett の方法など)の方法
対象読者:
- Excelを初めて使う方
- 実験データの分析を主にExcelで行いたい方
- 統計学の基礎を学びたい方
この記事を読むメリット:
- 具体的な手順と図で、誰でも簡単に実践できる
- 統計学の専門用語をできるだけ避け、わかりやすく解説
- よくある質問や注意点についても解説
※本記事の注意点は下記です。
- 手順の説明に注力するため、各手順の意味の解説は最小限にします。
- ※の赤字で記載している補足は、読まなくても本記事の理解には支障ありません。
- 超初心者を対象とする都合上、説明を極力簡単にするために不正確な表現を使用する場合があります。
2群比較
数値の入力
今回は例として「何も処理をしていないマウス (無処理マウス)」と「薬剤Aを投与したマウス (薬剤A投与マウス)」のある時点での体重を比較します。体重の数値 (グラム) は適当に考えました。エクセル初心者は下記の表をコピペして練習してください。
| 無処理マウス | 薬剤A投与マウス |
| 25 | 25.2 |
| 24.2 | 26 |
| 25.8 | 25.9 |
| 25.2 | 28.1 |
| 24.8 | 26.4 |
| 27.7 | |
| 27 | |
| 28.4 | |
| 29.2 |
得られた体重の測定値を下記の図の用に入力します。無処理マウスは5個体、薬剤A投与マウスは9個体分のデータです。
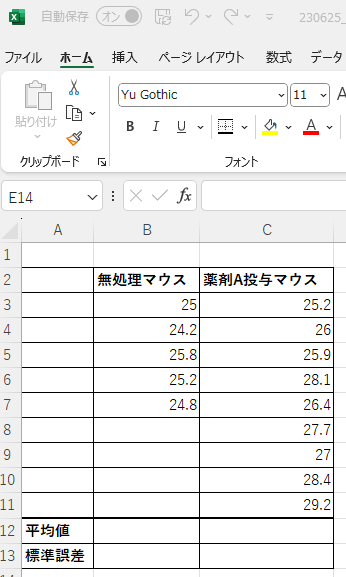
平均値を求める
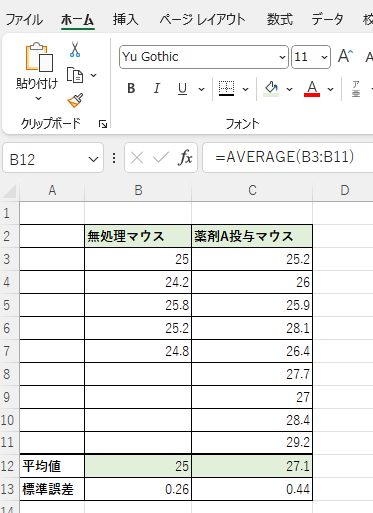
グラフに表示させる「各群の体重の平均値」を求めます。まずは無処理マウスの平均値から求めます。平均値を表示したいセルに
「=AVERAGE(各群の数値が含まれるセル全部)」
を入力します。手入力をすると間違えるので、上の式をコピペして入力してください。図のように空のセル (B8:B11) が式の選択範囲に含まれていても問題ありません。平均値の結果には反映されません。
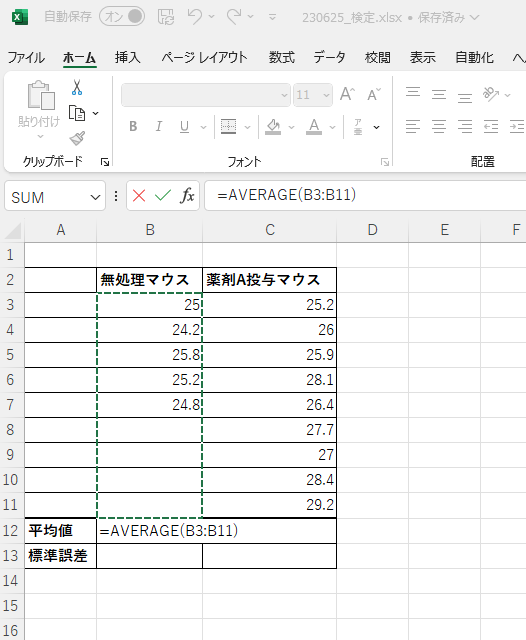
薬剤A投与マウス群の平均値も同様の手順で求めます。無処理マウスの平均値を求めたB12のセルをC12にコピペしても式が入力されます。式の入力をコピペした場合は、数値の選択範囲が合っているか確認しましょう。
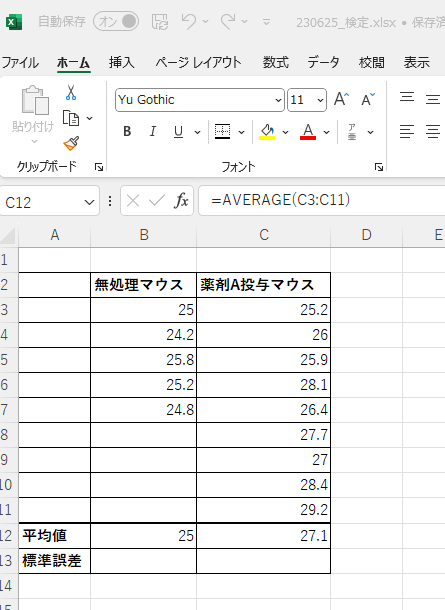
標準誤差を求める
エラーバーとして示す標準誤差を求めます※。まずは無処理マウスからです。
標準誤差を表示させたいセルに
「=STDEV(各群の数値が含まれるセル全部)/SQRT(COUNT(各群の数値が含まれるセル全部))」
を入力します。平均値の算出時と同様、空のセルが選択範囲に含まれていても問題ありません。
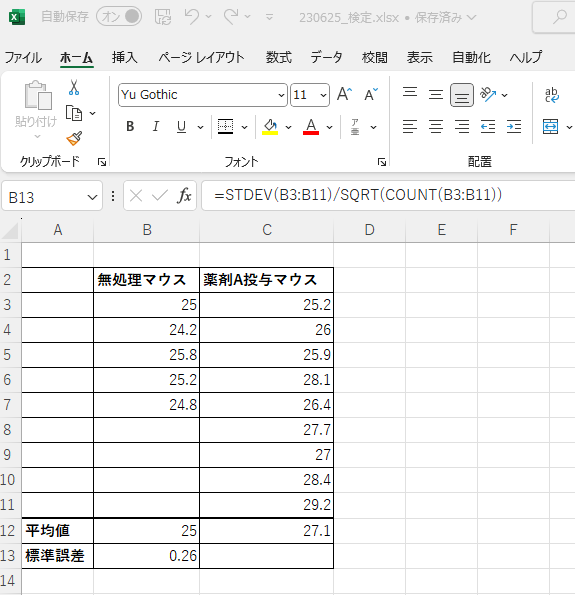
※エラーバーとして使用されるものには「標準偏差」と「標準誤差」があります。両者の使い分けは下記のリンク先などをご参照ください。今回は「無処理マウス」と「薬剤A投与マウス」の平均値を比較したいので、標準誤差をエラーバーとして使用します。
次に薬剤A投与マウス群の標準誤差を求めます。平均値と同様、セルをコピペすれば標準誤差の式もコピペできます。

グラフの作成
グラフを作成するために、「各群の名前」と「各群の平均値」(緑色のセル) を同時に選択します。WindowsならControlキーを押しながら選択することで、離れた位置にあるセルも同時に選択されます。
名前と平均値を同時に選択した状態で
Excel の「挿入」タブ→グラフの選択 (下記の写真は「2-D縦棒」の「集合縦棒」グラフを選択)
を行います。下記の図のように、各群の名前と平均値が表示されたグラフがExcel表中に挿入されます。

グラフへのエラーバーの挿入
作成したグラフに標準誤差をエラーバーとして挿入します。
グラフを選択 > グラフ要素を追加 > 誤差範囲 > その他のオプション > 誤差範囲のオプション > 誤差範囲 > ユーザー設定 > 値の指定
を選択します。

「正の誤差の値」と「負の誤差の値」の両方に対して、標準誤差が表示されているセル (B13, C13) をまとめて選択します。
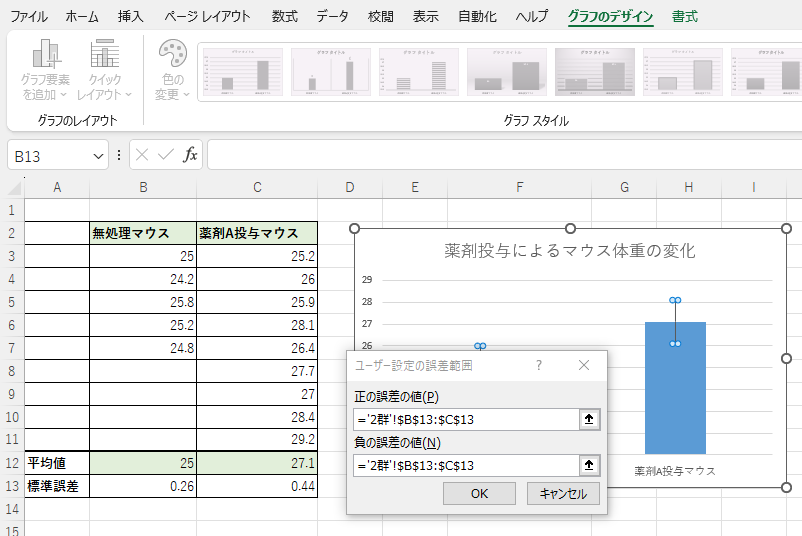
グラフに標準誤差の値が反映されたエラーバーが表示されます。

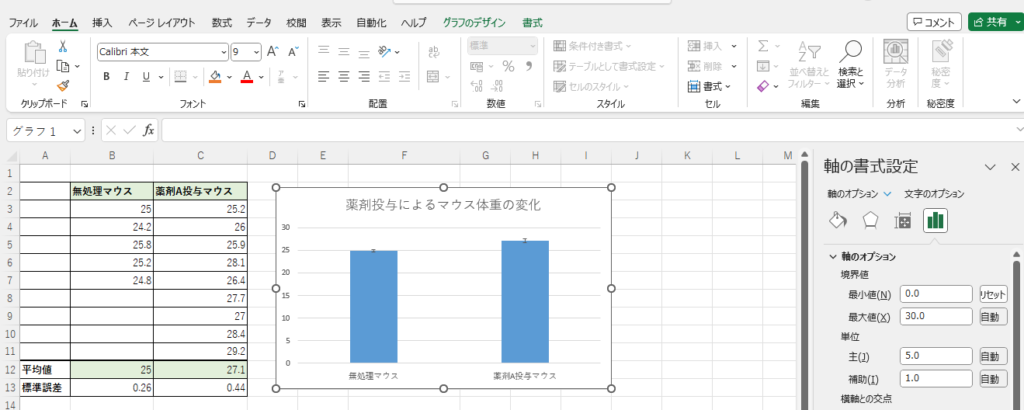
上のグラフは縦軸の最小値が23になっています。それを0にします。
縦軸をダブルクリック > 軸の書式設定 > 軸の最小値 > 境界値 > 最小値を0
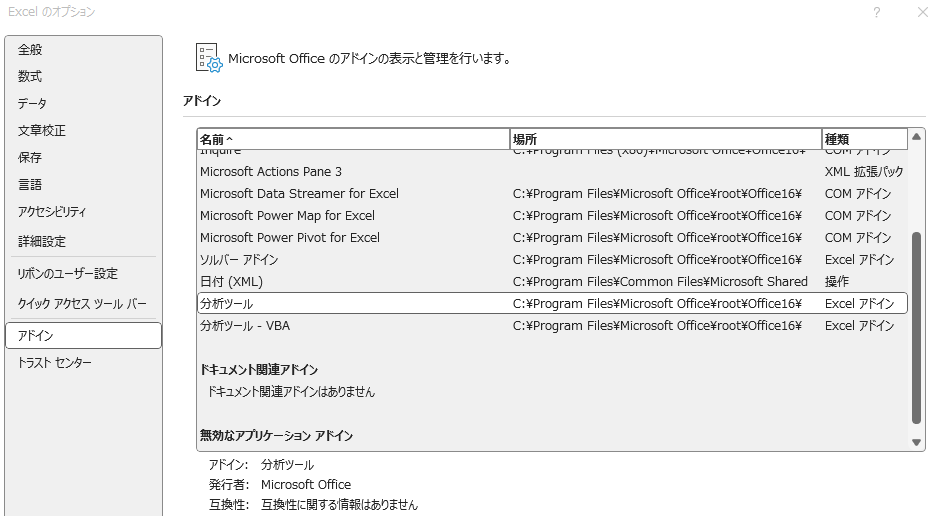
分析ツールの表示
統計学的な検定を行うために、分析ツールをExcelのタブに表示させます。下記サイトの記載が参考になります。

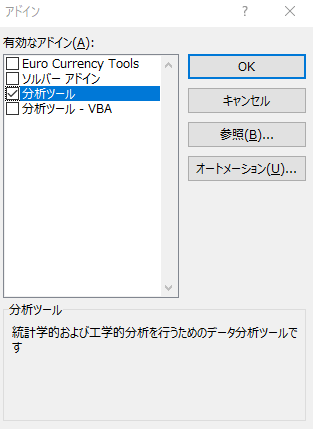
ファイル > オプション > アドイン > 設定 > 「分析ツール」に✓ > OK
以上の作業で、Excelの「データ」タブに「データ分析」が表示されます。
F検定を行う
2群間の比較としてまずF検定を行います※。非常に簡単に言うと、「F検定は2群の分散 (ばらつき) が等しいかを判定する検定」です。下記サイトの記載が参考になります。

※厳密には、まず「比較する2群のデータが正規分布するか」を確かめる必要があります。正規分布しているかを確かめる検定としては「Shapiro–Wilkの検定」などがありますが、Excelでこの検定を実施することは (多分) できません。具体的なフローチャートは下記画像を参照してください (本当はもっと細かくしないといけないかも)。

この記事では、2群のデータのいずれも正規分布していると仮定して、Excelで実行可能な前述のF検定や後述のt検定を行っています。
厳密には、「2群のデータのうち、いずれかが正規分布していない」場合は、後述のt検定は使用できません。その場合は「Wilcoxonの順位和検定」などを行います。下記サイトの記載が非常に参考になります。
また比較する2群が「対応がある」場合はF検定を行う必要はありません。「対応がある」とは、「あるマウスに薬剤を投与して、投与前後の体重を比較する場合」などです。前後の動物・人・サンプルが同一の場合と考えればOKです。この記事の「無処理マウス」と「薬剤A投与マウス」は別の個体を想定しているので、今回はF検定を行います。下記の動画が参考になります。
F検定を行うには
データ > データ分析 > F検定: 2標本を使った分散の検定

変数1の入力範囲 > 無処理マウスのデータを選択
変数2の入力範囲 > 薬剤A投与マウス
出力先 > 同じワークシート内で結果を表示させたいセル
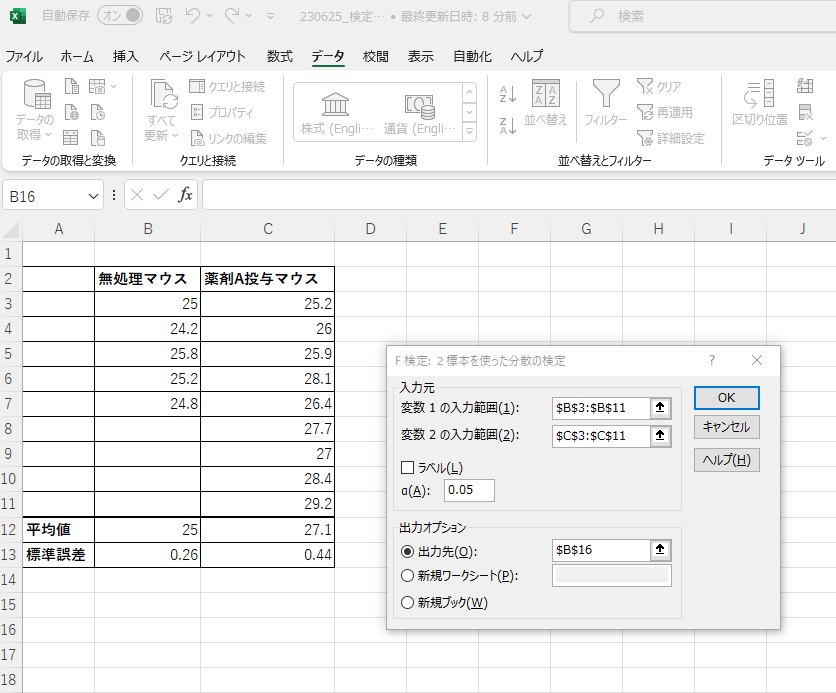
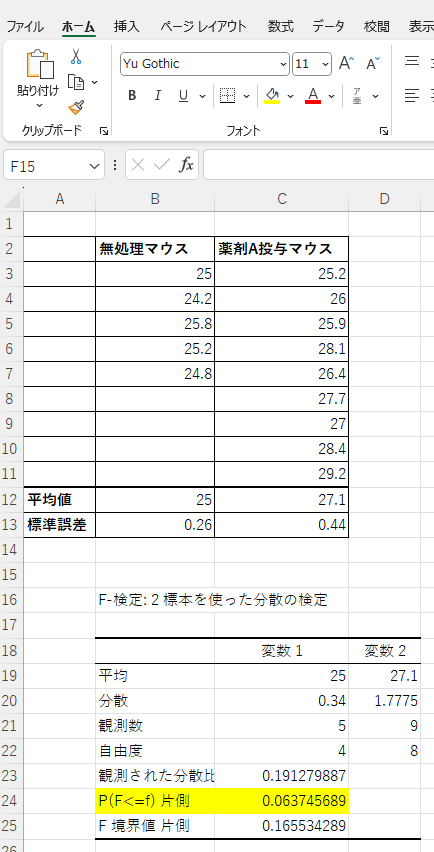
F検定の結果が出力されます。「P(F<=f) 片側」(黄色のセル) の値によって、後述するt検定の種類が変わります※。
「P(F<=f) 片側」> 0.05 → 2群の分散は等しい (等分散) → t検定:等分散を仮定した2標本による検定
「P(F<=f) 片側」< 0.05 → 2群の分散は等しくない →t検定:分散が等しくないと仮定した2標本による検定
今回の「P(F<=f) 片側」は~0.064と > 0.05 だったので、下記では「 t検定:等分散を仮定した2標本による検定」を行っていきます。
※対応がある2群間を比較する場合は、F検定を行わず「t検定:一対の標本による平均の検定」を行います。下記サイトが参考になります。

t検定を行う
t検定 (等分散) を行うには
データ > データ分析 > t検定:等分散を仮定した2標本による検定
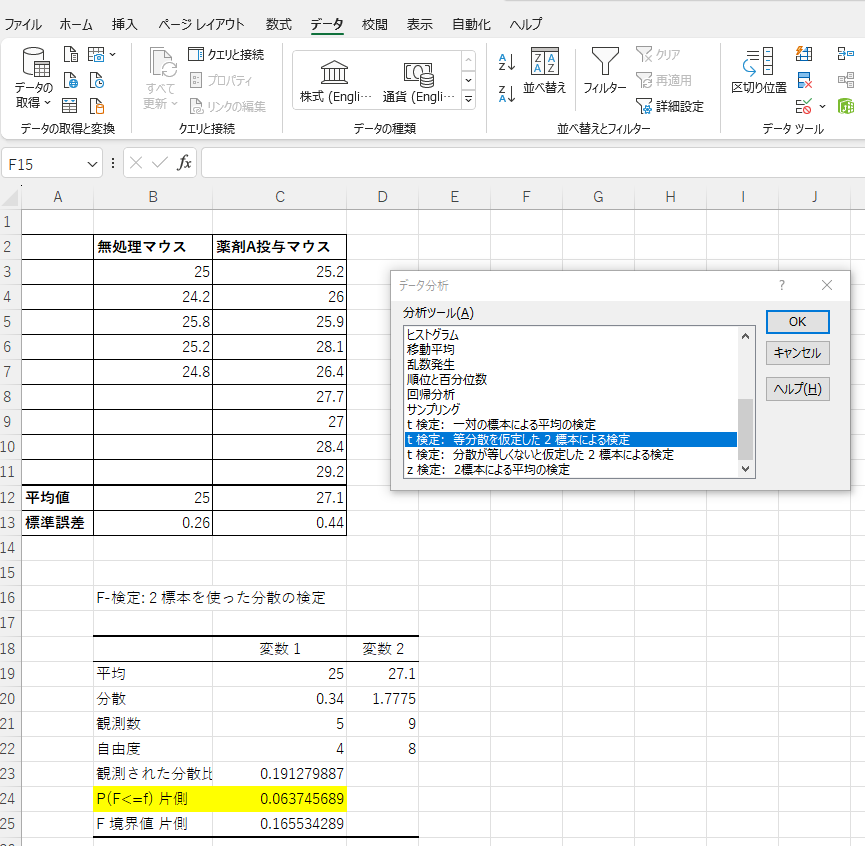
F検定の時と同様に、
変数1の入力範囲 > 無処理マウスのデータを選択
変数2の入力範囲 > 薬剤A投与マウス
出力先 > 同じワークシート内で結果を表示させたいセル
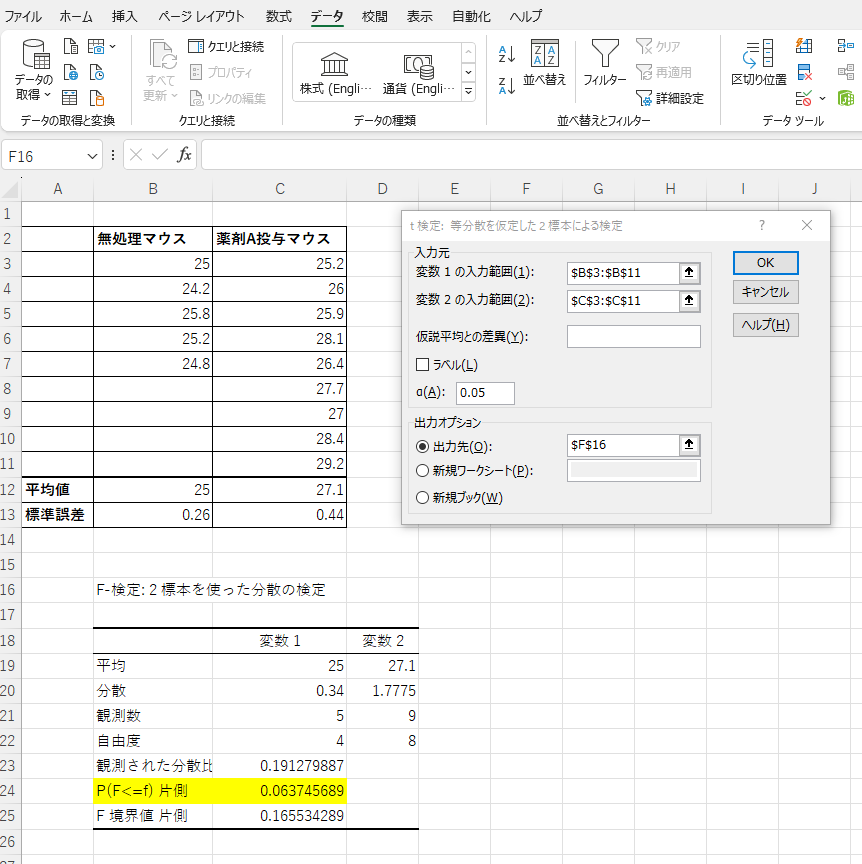
t検定の結果が出力されます。「P(T<=f) 両側」(黄色のセル) の値で有意差があるか判断します※。
「P(T<=f) 両側」> 0.05 → 有意差なし
「P(T<=f) 両側」」< 0.05 → 有意差あり
今回は「P(T<=f) 両側」が~0.006だったので、両群の平均値には有意差ありと判断します。

※「P(T<=f) 両側」ではなく「P(T<=f) 片側」の値を判断する場合もあります。下記のサイトが参考になります。
グラフをPowerPointに貼る
Excelで作成したグラフをPowerPointにコピペします。ペーストするときは
右クリック > 貼り付けのオプション > 図
とします。こうすることで単なる図としてペーストすることができるので、グラフのデザインが崩れなくなります。
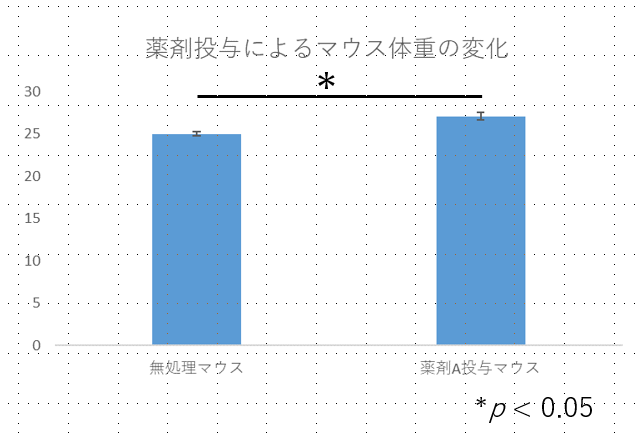
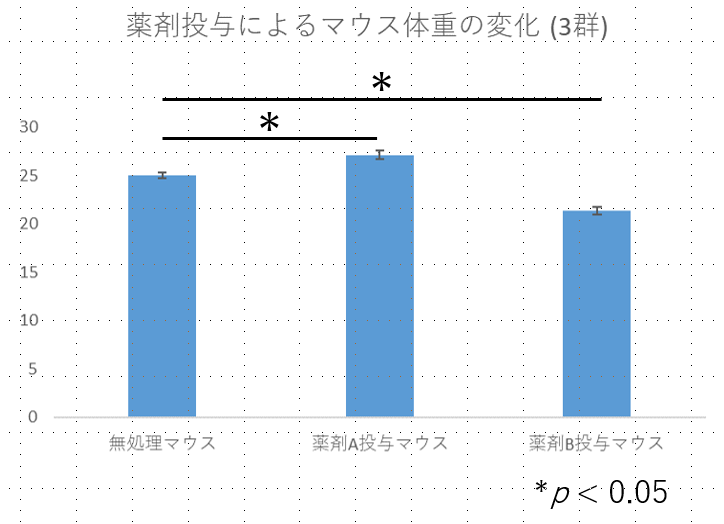
グラフ中に「*(アスタリスク) 」や「*p < 0.05」などの表記をいれて完成。
多群比較 (3群以上)
数値の入力
3群比較では例として、2群比較で使用した「何も処理をしていないマウス (無処理マウス)」と「薬剤Aを投与したマウス (薬剤A投与マウス)」の群に加えて、「薬剤Bを投与したマウス (薬剤B投与マウス)」のデータを用います。必要に応じて、下記の表をExcel にコピペして練習してください。
| 無処理マウス | 薬剤A投与マウス | 薬剤B投与マウス |
| 25 | 25.2 | 21 |
| 24.2 | 26 | 20 |
| 25.8 | 25.9 | 20.1 |
| 25.2 | 28.1 | 22 |
| 24.8 | 26.4 | 23.2 |
| 27.7 | 20.1 | |
| 27 | 22.3 | |
| 28.4 | 22 | |
| 29.2 |
平均値を求める、標準誤差を求める、グラフの作成、グラフへのエラーバーの挿入
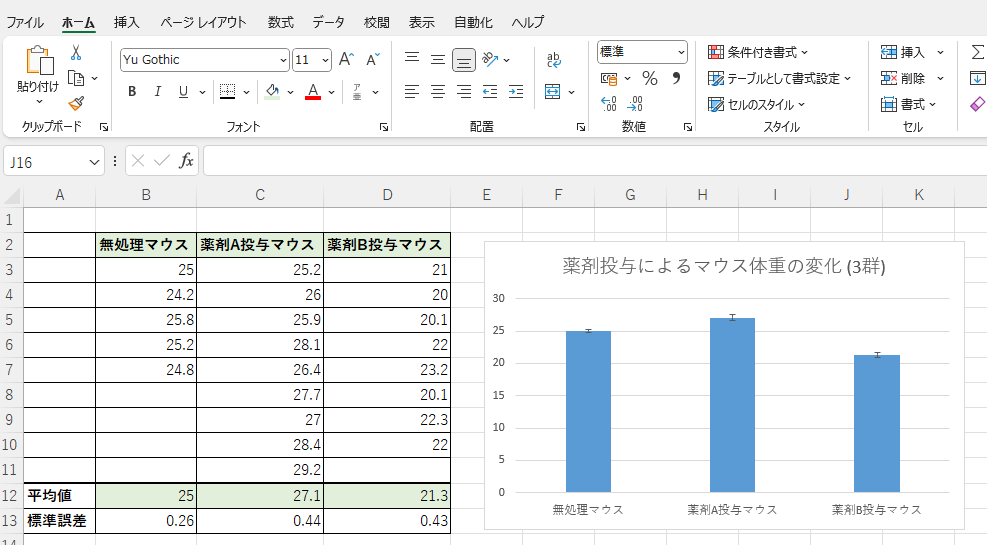
平均値、標準誤差、グラフ、エラーバーについては、2群比較と全く同様の手順になるので割愛します。上述の記載を参考に作成してください。最終的には下記の様なグラフができます。
検定方法を選択する
多群比較を行うにあたり、検定方法を選択する必要があります。超簡単に言うと、下記の2パターンです※。
色々な群間で比較したい → Tukeyの方法
対照群が1つあって、対照群と他群を比較したい → Dunnettの方法
今回のケースでは、対照群 (無処理マウス) と他群 (薬剤A投与マウス、薬剤B投与マウス) の比較を行いたいです。薬剤A投与マウスと薬剤B投与マウスの比較に興味がありません。従ってDunnettの方法で検定します。
もし各群が「毛色が白色のマウス」・「黒色のマウス」・「茶色のマウス」であり、全ての群間の比較に興味があるならTukeyの方法を選択します。
Tukeyの方法やDunnettの方法については下記サイトが大変参考になります。
※2群間の比較と同様、他群比較でも本来は下記手順のような流れになります (もっと細かいかも)。本記事では、例として挙げている3群が正規分布・等分散していることを仮定して進めています。

検定を行う
多群比較のための検定をExcelで行うことは (多分) できません。
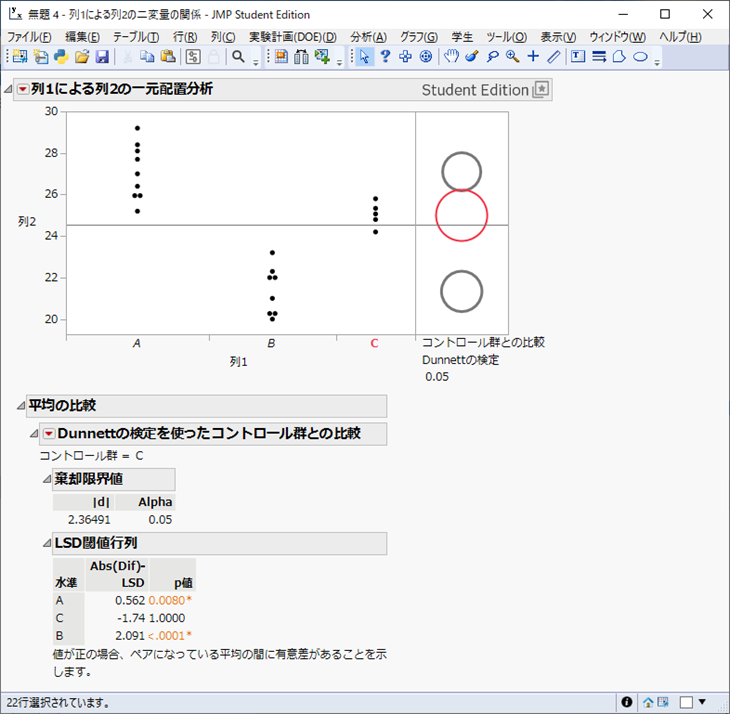
下記の記事を参考に、大学生なら無料で使えるJMP Student Editionを使用して多群比較を行ってください。
リンク先の記事では、下記のようにグループ名を設定しています。
- C: 無処理マウス
- A: 薬剤A投与マウス
- B: 薬剤B投与マウス
得られた結果を解釈します。今回の場合、
(C,A) の検定結果が「P < 0.05」→ 無処理マウスと薬剤A投与マウスに差がある
(C,B) の検定結果が「P < 0.05」→ 無処理マウスと薬剤B投与マウスに差がある
グラフをPowerPointに貼る
2群間の比較の時と同様、Excelで作成したグラフをPowerPointにコピペして完成させます。
まとめ
Excelでのグラフ作成から統計検定までの手順を、初心者の方にもわかりやすく解説しました。
棒グラフとエラーバーの作成、2群比較、多群比較など、具体的な方法を図解で示しました。
この記事を参考に、Excelで効率的にデータ分析を行いましょう
関連記事
↑多群比較を行うことができるソフトウェアである R と GraphPad Prism を比較した記事です。
↑現役大学教員の私が実際に使用している「研究の効率アップに役立つウェブ・PCツール」を紹介している記事です。グラフ作成、統計解析に使用できる GraphPad Prism の紹介もあります。







コメント